[LeetCode] Longest Cycle in a Graph

문제

• https://leetcode.com/problems/longest-cycle-in-a-graph/
• 난이도: Hard
• 토픽: DFS, Graph, Topological sorting

그래프가 주어지면 그래프 내의 사이클중 제일 길이가 긴 사이클 길이를 구하는 문제이다.

 

접근방법

그래프에서 사이클을 감지하는 가장 간단한 알고리즘으로 Floyd의 거북이 & 토끼 알고리즘이 있다.

 

Floyd의 거북이 & 토끼 알고리즘

1. 거북이와 토끼를 시작점에 놓고 거북이는 한 번에 1칸 움직이고, 토끼는 한 번에 2칸 움직인다.
2. 그래프에 사이클이 있다면 토끼와 거북이는 어느 한 지점에서 반드시 만나게 된다.

사이클을 감지하는 건 알겠는데, 어떻게 하면 사이클의 길이를 측정할 수 있을까?

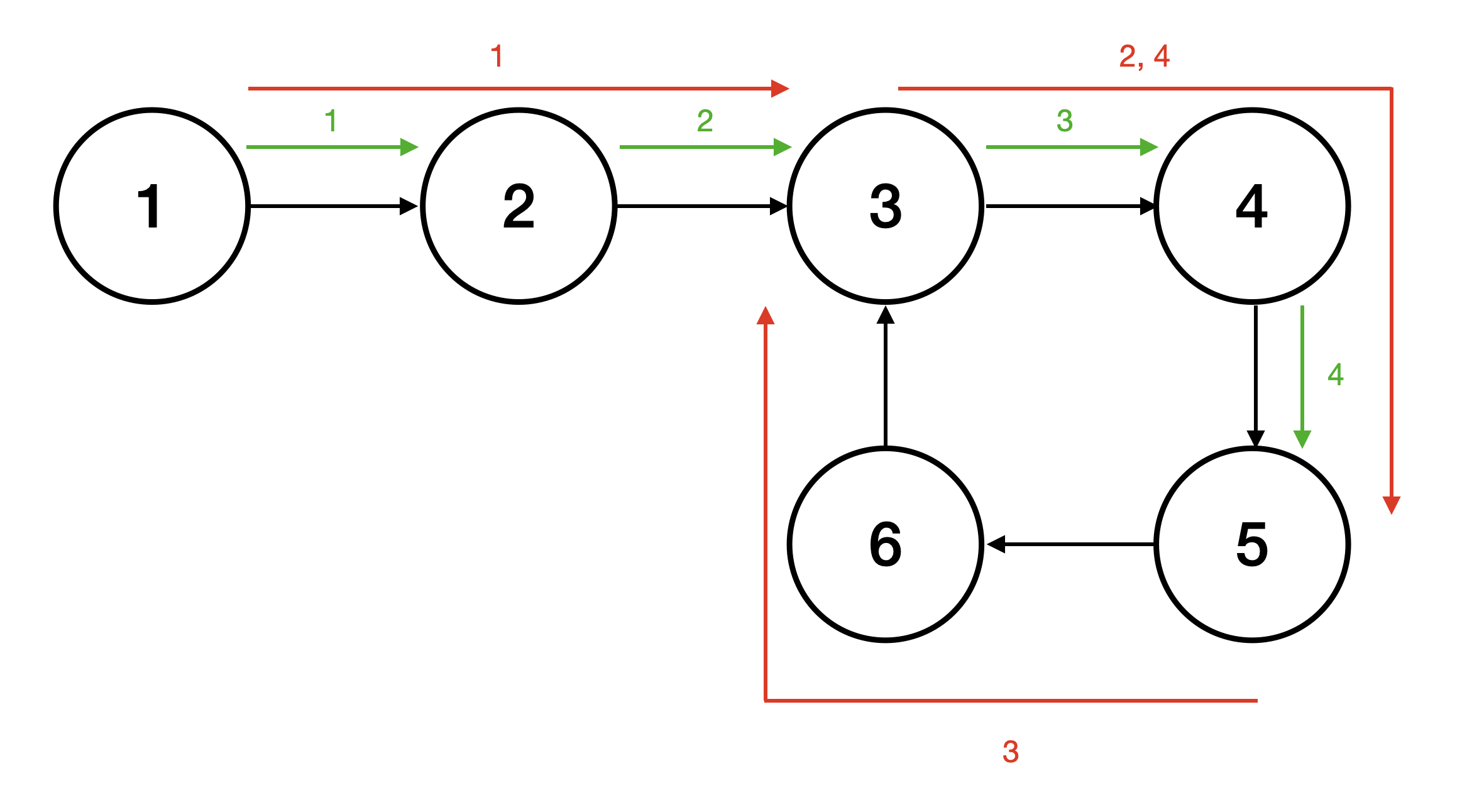
위의 그래프에서 거북이와 토끼는 4번 이동하여 노드 5번에서 만나게 된다.

거북이와 토끼가 만나면 거북이를 다시 시작노드인 1로 이동시키고, 이제부터 거북이와 토끼를 한 칸씩 움직인다.

움직이기 시작하고 첫 번째로 거북이와 토끼가 만나는 지점이 바로 사이클의 시작점이다.

[증명]
L: 그래프의 시작점부터 사이클 시작점까지의 길이
n: 사이클의 순환 길이
x: 사이클 시작점으로부터 거북이가 이동한 길이(=사이클 시작점으로 부터 토끼와 만나는 노드의 길이)
c1, c2: 거북이가 사이클을 회전한 횟수, 토끼가 사이클을 회전한 횟수

거북이와 토끼가 만나는 시점에서
거북이가 이동한 길이는 L + c1 * n + x
토끼가 이동한 길이는 L + c2 * n + x 이다.

토끼는 거북이의 2배로 움직이므로
2(L + c1*n + x) = L + c2*n + x 이고, 이 식을 정리하면
L  = (c2 - 2c1)n  - x 이된다.

토끼가 사이클의 시작점으로 이동해야하는거리는 n - x
시작점으로 간 거북이가 사이클의 시작점으로 이동해야하는 거리는 L이다. 
(c2 - 2c1)은 회전한 횟수이고, 사이클에서 아무리 회전해도 원점으로 돌아오므로 (c2 - 2c1) * n 은 n이다.
따라서 L = n - x 가 성립하므로, 거북이와 토끼는 사이클의 시작점에서 만나게 된다.

 

풀이

Floyd의 거북이 & 토끼 알고리즘을 사용한다.

class Solution:
    def longestCycle(self, edges: List[int]) -> int:
        answer = 0
        visited = [False for _ in edges]
        for start in range(len(edges)):
            tortoise, hare = start, start
            while tortoise >= 0 and hare >= 0 and edges[hare] >= 0 and not visited[tortoise]:
                tortoise = edges[tortoise]
                hare = edges[edges[hare]]
                if tortoise == hare:
                    break
            else:
                continue    # No Cycle
            
            # Find Cycle Start Node
            tortoise = start
            while tortoise != hare:
                tortoise = edges[tortoise]
                hare = edges[hare]

            visited[tortoise] = True
            tortoise = edges[tortoise]
            cycle_length = 1
            while tortoise != hare:
                tortoise = edges[tortoise]
                visited[tortoise] = True
                cycle_length += 1
            
            answer = max(answer, cycle_length)
        
        return answer if answer > 0 else -1

1. 토끼와 거북이 알고리즘을 통해 사이클이 있는지 없는지 체크한다. 사이클이 없으면 continue로 다음 노드를 탐색한다.
   (중요) 이미 방문했던 사이클 노드가 있으면 아래는 똑같은 연산을 반복하는것이기 때문에 더 이상 찾지 않고 다음 루프로 넘어간다.
2. 거북이를 시작점으로 다시 놓고 거북이 토끼를 한 칸씩 이동하면서 사이클 시작점을 찾는다.
3. 시작점부터 시작해서 다시 시작점으로 돌아올때까지 사이클 길이를 구한다.
   (중요) 사이클 노드마다 방문 체크를 해서 반복으로 똑같은 사이클 길이를 구하지 않도록 한다.
4. answer와 비교하며 최대 길이를 구한다.