[LeetCode] Validate Binary Search Tree

문제

트리가 주어지면 이 트리가 정말 Binary Search Tree가 맞는지 판단하는 문제이다.

98.Validate Binary Search Tree

Binary Search Tree

BST는 아래와 같은 조건을 모두 만족하는 트리이다.

1. 해당 노드의 왼쪽 서브 트리의 값은 모두 해당 노드의 값보다 작아야한다.
2. 해당 노드의 오른쪽 서브 트리의 값은 모두 해당 노드의 값보다 커야한다.
3. 왼쪽 서브 트리, 오른쪽 서브 트리 모두 BST이다.

접근 방법

처음에는 정말 간단하게 생각해서 왼쪽 자식 노드의 값 < 현재 노드의 값 < 오른쪽 자식 노드의 값 인지 판단하는 함수를 만들어 재귀적으로 판단하면 되겠다 생각해서 아래와 같이 작성했다.

def is_valid_bst(self, node:TreeNode):
        if node.left and node.right:
            return self.is_valid_bst(node.left) and node.left.val < node.val < node.right.val and self.is_valid_bst(node.right)
        elif node.left:
            return self.is_valid_bst(node.left) and node.left.val < node.val
        elif node.right:
            return node.left.val < node.val < node.right.val and self.is_valid_bst(node.right)
        
        # 리프노드라면
        return True

하지만 아래와 같은 반례가 있었다.

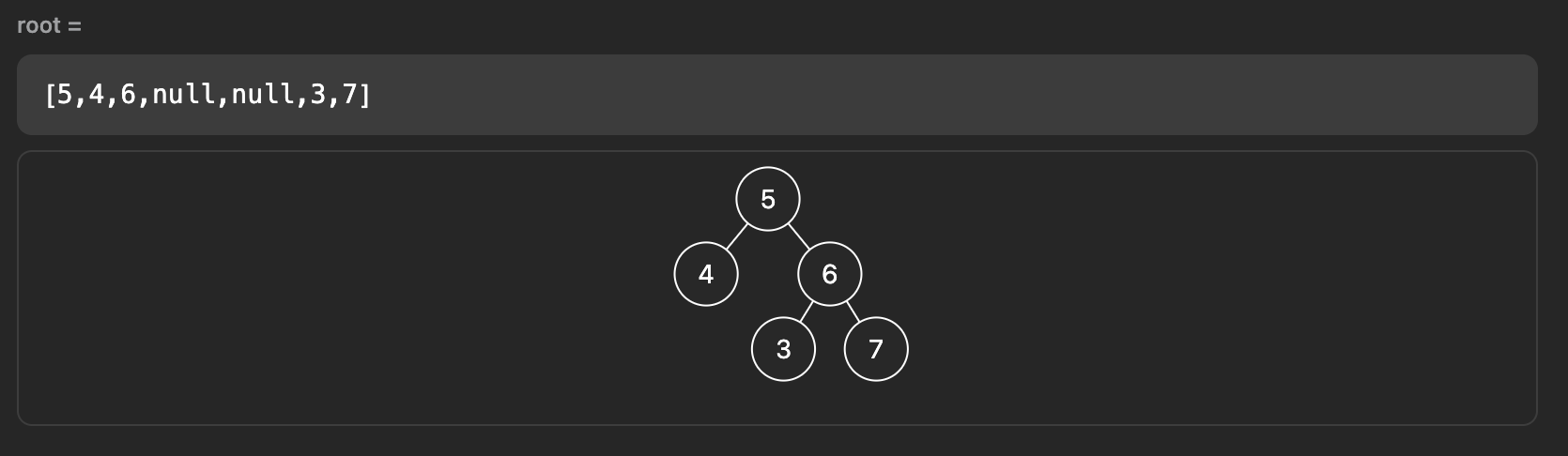
4 < 5 < 6을 만족하고 3 < 6 < 7 을 만족하지만 오른쪽 서브 트리에 왼쪽 서브 트리에 존재하는 4보다 작은 3이 존재하기 때문이다.

 

어떻게 풀어야 하나 몇 번 시도해보다가 Dicussions에서 키워드를 얻었다.

Inorder Traversal을 하면 조회 순서가 오름차순이라는 것이다.

생각해보면 그럴 수 밖에 없다. 왼쪽 서브 트리 -> 루트 -> 오른쪽 서브 트리 순으로 탐색하므로 BST라면 먼저 조회하는 값이 제일 작은것을 보장할 수 있다. 이렇게 간단한걸 헤맸다니.. 아무튼 간단하게 해결할 수 있는 문제였다.

풀이

class Solution:
    def inorder_traversal(self, node:TreeNode, result: List[int]):
        if node.left:
            self.inorder_traversal(node.left, result)
        result.append(node.val)
        if node.right:
            self.inorder_traversal(node.right, result)
        
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        result = []
        self.inorder_traversal(root, result)
        
        for i in range(1, len(result)):
            if result[i] <= result[i - 1]:
                return False
        return True